我的开源1. 红黑树的性质
红黑树是一种自平衡的二叉搜索树，有如下一些性质：
- 红黑树是一棵平衡二叉搜索树，其中序遍历单调不减。
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(也有称外部节点的，目的是将红黑树变为真二叉树，即 NULL 节点，空节点)是黑色的。
- 每个红色节点的两个子节点都是黑色。(换句话说，从每个叶子到根的所有路径上不能有两个连续的
红色节点) - 从根节点到每个叶子的所有路径都包含相同数目的黑色节点（这个数值叫做黑高度）。
由于每个叶子节点黑高相同且不存在相邻红节点，所以每个叶节点的高度都不会超过其他叶节点高度的两倍，所以可以认为它是相对平衡的。
红黑树主要通过染色和旋转两种方式实现自平衡。
染色： 不解释，就是把红的变成黑的，黑的变成红的。
旋转： 分为左旋和右旋。
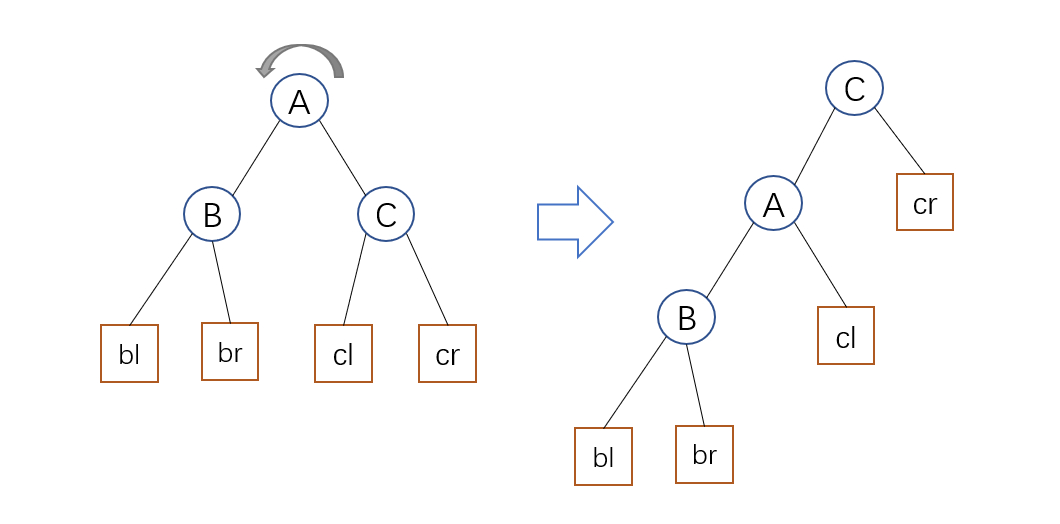
左旋的操作如下图所示，右旋类似，旋转操作不破坏二叉搜索树的性质，只是改变了树的结构，让被旋转的孩子节点成为新的根节点。
2.红黑树插入
首先对于红黑树的插入，插入的节点必须为红节点。
插入之后，若插入节点的父节点为黑节点，则红黑树本身的性质并不改变（每个叶子结点黑高相等且不包含相邻红节点），直接插入即可。
若插入节点的父节点为红节点，则需要进行修正。首先设待修复的节点为z，将z初始化为当前插入节点。
修正操作的步骤如下：
- 先看当前节点z叔节点是否为红色
若叔节点为红色，将叔节点和父节点染成黑色，然后将当前节点z设为祖父节点。 - 若当前节点的叔节点为黑色
A. 首先检查当前节点z与其祖父节点是否在一条直线上，若不在一条直线上通过旋转父节点让其在一条直线上，当前节点z设为旋转前z的父节点。(若本身在一条直线上则忽略这一步)。
以z的叔节点为祖父节点右儿子为例，如下所示。
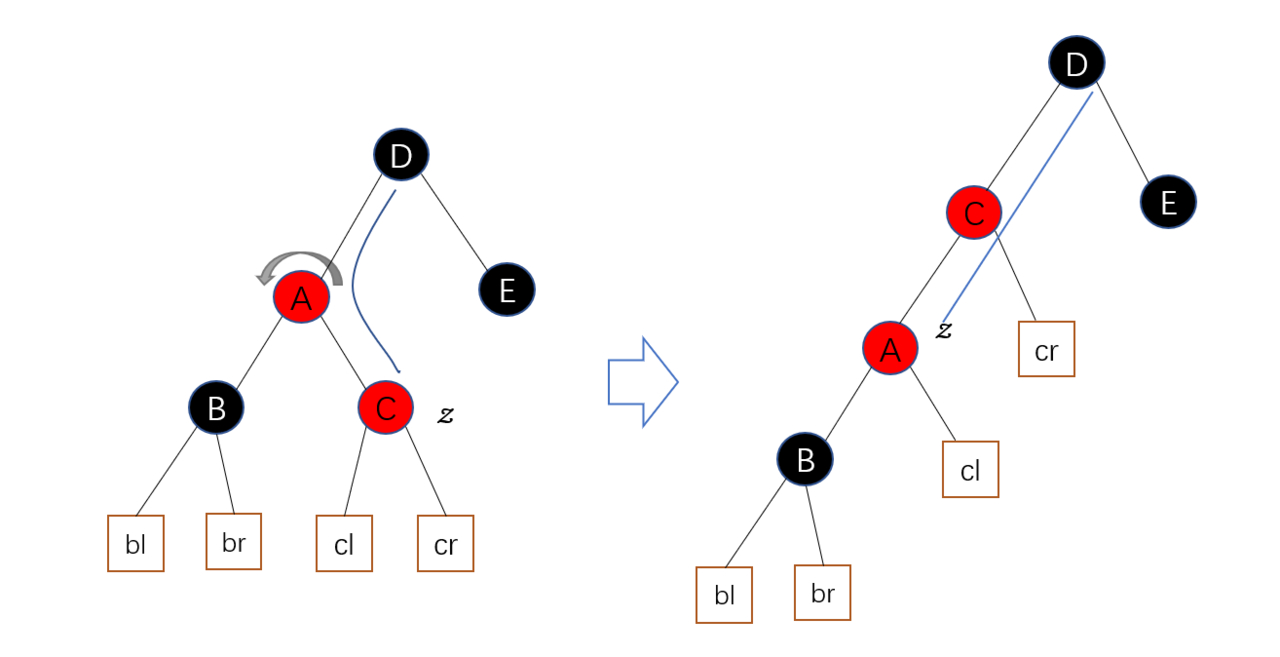
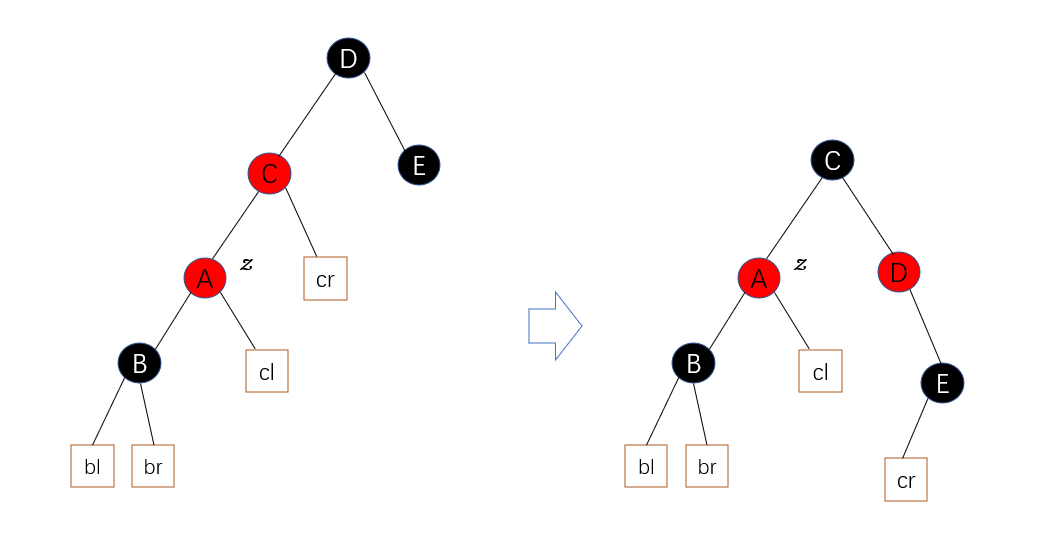
B. 此时当前节点z与其祖父节点已经在一条直线上 , 将z的父节点染成黑色，z的祖父节点染成红色，左旋(右旋)祖父节点使父节点取代原先祖父节点的位置。
2.红黑树删除
红黑树的删除可谓是一个难点，具体可以分为两个步骤：
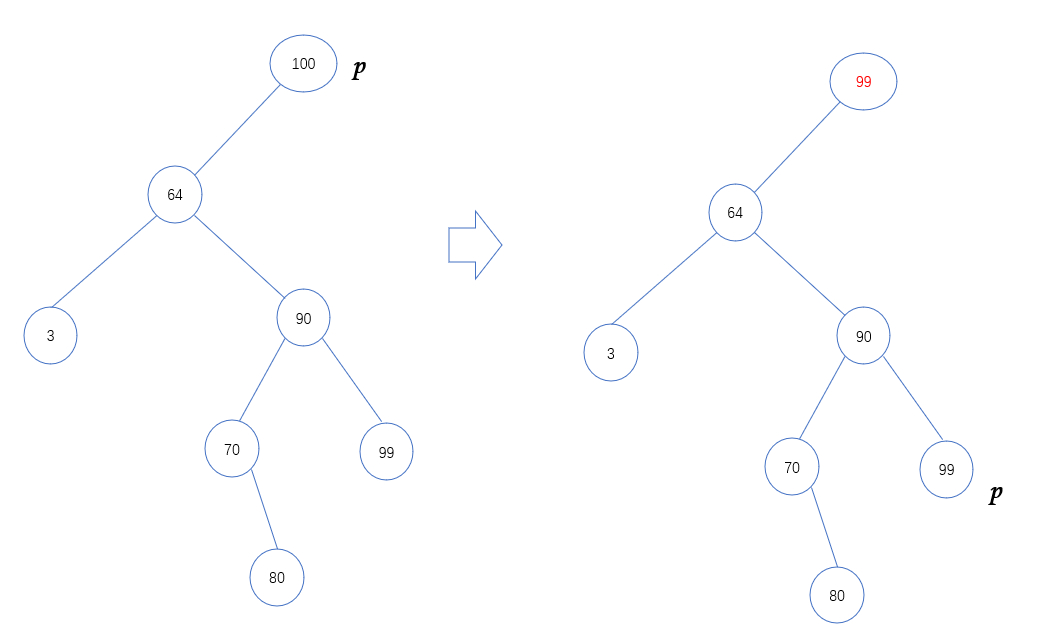
- 找到待删除的节点设为当前节点，若当前节点不为叶子结点，通过用他的直接真后继（右子树最左节点）或直接真前驱（左子树最右节点）去替换它直到当前节点为叶节点。
如图，在当前节点有右子树的情况下可以进行如下替换，若删除的节点值为 64(p)，经过两次替换将待删除节点转化为叶节点。
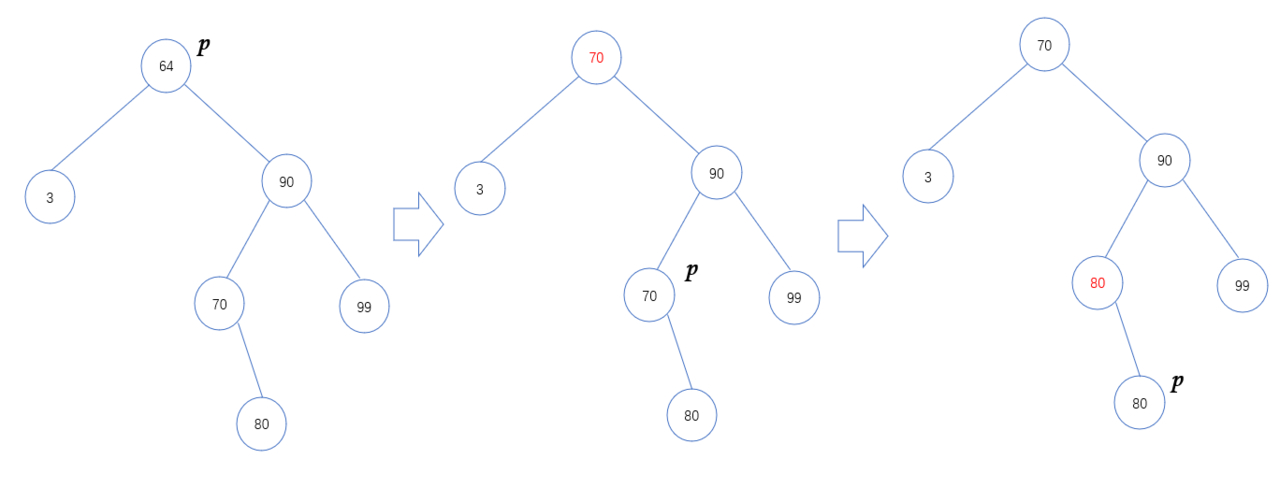
若当前节点没有右子树，则用其直接真前驱进行替换。
Tips:
在红黑树中，若一个节点只有左孩子或右孩子，则其左孩子或右孩子一定为叶子节点且为红节点，所以这里代码里也可以直接写成用左孩子替换,但写成直接前驱的形式便于测试在没有进行失黑修复的情况下代码的正确性（踩过的坑)。 - 经过第一步，此时需要删除的节点已经转移到一个叶子节点上，若该节点为一个红节点，则皆大欢喜，直接删除即可，若为黑节点，若直接删除，必然带来的一个问题是该节点此时变成一个黑色的 NIL 节点，而这个 NIL 节点的黑高度必然比原来的高度少 1，此时需要进行失黑修复使红黑树重新达到平衡。
失黑修复的本质是通过旋转与染色，从别处借一个红色节点节点来染成黑色使树重新达到平衡。
这时候有四种情况，直接引用算法导论的原图：
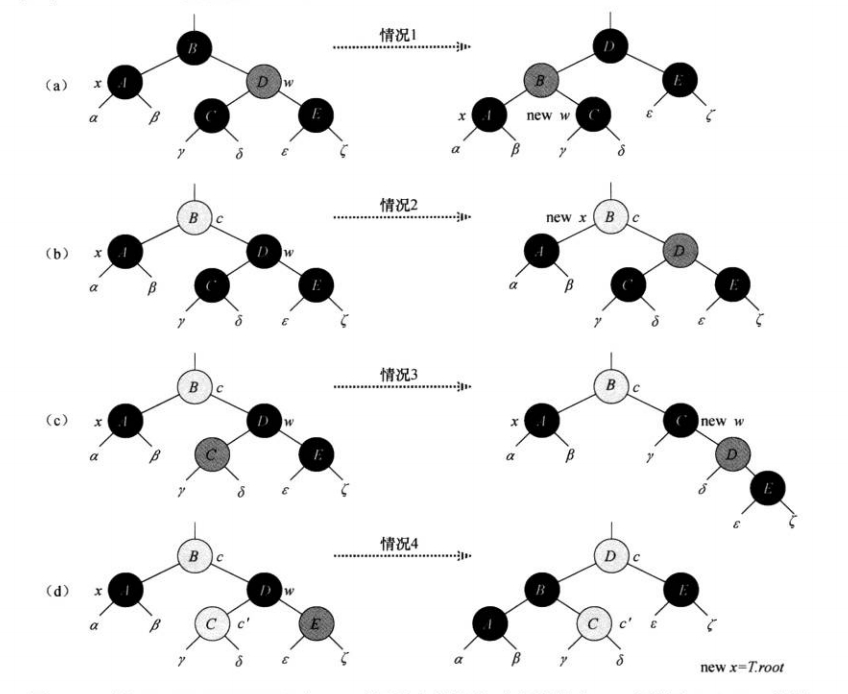
首先用两个节点分别指向当前节点x和当前节点的兄弟w，当x的颜色为红色或x为 root 时终止循环。
Case A： 若兄弟节点w为红色，交换兄弟节点和父节点的颜色，然后左旋（右旋）父亲节点使兄弟节点变成父节点，然后将w更新为x的新兄弟也就是之前 w 的左孩子。此时 Case A 必然转化为 Case B。
可以理解为兄弟将自己的红节点移交给了父亲，然后再找父亲要.
Case B： 若兄弟节点为黑色且兄弟节点的子节点均为黑色，将兄弟节点设为红色，当前节点x更新为x的父节点。
可以理解成当前节点的兄弟和侄子都拿不出红节点时，兄弟自己染红，黑高减 1，维持父节点左右黑高平衡的同时，把锅甩给父亲，让父亲节点进行失黑修复，此时有两种情况，若父亲为红节点，将父亲涂黑，循环终止，修复完成，否则父亲必须再想办法解决，要么找它的兄弟借，要么找它的侄子借。
Case C： 若当前兄弟的侄子有红节点
首先若当前节点侄子与当前节点父节点不在一条直线上，将其旋转到一条直线上便于后续操作，见图中 case3。
此时先将父节点染黑，左旋（右旋）时充当左（右）子树使其高度 +1，在原来父亲节点所在位置以及兄弟节点所在位置保持颜色不变即可。
最终结果是侄子节点由红色变成了黑色，父节点变成了黑色，兄弟节点变成了父亲的颜色最终保持子树的高度不变（内部交换提供了一个红节点）。
失黑修复伪代码如下：
3.红黑树查找
与一般二叉搜索树相同，这里不再赘述。
4. Code
实现了 RB_tree 这个类，简单实现了插入删除和查找的功能，详见 github。
template <class T>
class RB_tree {
public:
RB_tree() {
root = nullptr;
}
~RB_tree() {
clear_tr();
}
bool insert_val(T val);
bool search_val(T val);
bool delete_val(T val);
void clear_tr();
void print_t();
int tsize();
protected:
struct RB_node;
RB_node* root;
int _size;
RB_node* left_rotate(RB_node* rbnode);
RB_node* right_rotate(RB_node* rbnode);
RB_node* findv(T v,RB_node*& pre);
void delete_t(RB_node *r);
inline RB_node* bro(RB_node* rbnode) {
return rbnode == rbnode->p->lc ? rbnode->p->rc : rbnode->p->lc;
}
bool init(T v);
void solve_lost_black(RB_node* rbnode);
};
见 Github ：https://github.com/YaoCheng8667/RBTree_by_cpp
5. Reference
《算法导论》原书第三版 机械工业出版社