我的开源1. 问题描述
KMP 算法解决的主要是字符串匹配问题，如在字符串 Str 中找寻子串 Pattern 是否存在，如果存在，输出 Pattern 在 Str 中出现的位置，否则输出 -1 ；
因为 abcx[aba]bx 包含了子串 aba ，所以算法返回 aba 出现的位置 4 。
2. KMP 算法
2.1 时间空间复杂度
若采用暴力搜索的方式解决这个问题，则每次找寻以 Str[i] 开头的子串是否为 Pattern ，时间复杂度为 O(MN) 其中 M 为 Str 长度， N 为 Pattern 长度。
KMP 算法可以用 O(M+N) 的时间复杂度和 O(N) 的空间复杂度来解决这个问题。
2.2 算法基本介绍
算法的关键是对于子串构造一个 Next 数组用于解决每次子串不匹配时，都要返回子串开头重新匹配的问题。
解决方式是在匹配一个字符时，若以该字符前一个字符为结尾的后缀串与子串 Pattern 的前缀相同时，该（后缀/前缀）串无需在目标字符串中重新比较。
例如：
Str： abcabcabddef
Pattern: abcabd
- 若比较至如下步骤：
此时 Str 与 Pattern 前 5 个字符均相等，要比较 c 和 d 。
因为 [(ab)c(ab)] 以 b 结尾的后缀子串 (ab) 同时也是 Pattern 的前缀，所以下一次比较时 (ab) 无需重新比较。
- 此时跳转至比较如下比较步骤：
2.3 Next 数组构建
-
next 数组语义：
next 数组主要用作子串当前字符不匹配时指出下一个该匹配的字符的下标。
例如：
在上一节的例子中提到，如果 abcabd 中 d 不匹配，会去比较 c ,所以 next[5] = 3 ，就是第 5 个位置不匹配的话子串可以直接从第 3 个位置开始比较。
为了方便，我们设 next[0] = -1 。
有了 next 数组之后，每次比较 Str[i] 和 Pattern[j] 时，若 或Str[i] == Pattern[j] ，则比较两个串下一个位置，否则比较 Str[i] 和 Pattern[next[j]] ，若 next[j] == -1 ，表示 Str 中以 Str[i] 和其之前的子串中都不可能包含 Pattern 的一部分，此时也需要比较两个串下一个位置。 -
next 数组构建：
现在假设要求 Next[i] ，要保证的条件是以 Pattern[i-1] 为结尾的子串恰好为 Pattern 的开头，假设该符合条件的前缀为 S ，而这一条件可以划分为以下两个子条件：- Pattern[i-1] = S[S.length -1]
- Pattern[i-1-S.length : i-2] = S[ 0 : S.length - 2 ]
通俗的解释如下图：若黄色部分表示 Pattern 串第 i-1 个元素，橙色部分表示符合条件前缀的剩余部分，黄色部分和橙色部分都对应相等。
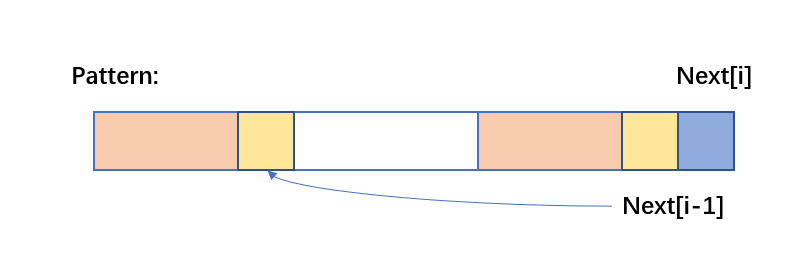
而根据 Next 数组的定义， Next[i-1] 指向的位置表示该位置以前的部分与以 Next[i-2] 为结尾的等长后缀是相等的（也就是橙色的部分相等）。
而此时如果 Pattern[Next[i-1]] == Pattern[i-1] （黄色部分相等），则满足了上面两个条件，那么 Next[i] = Next[i-1] + 1 。
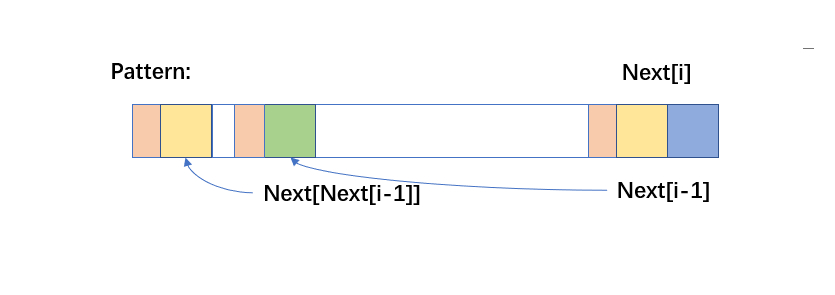
如果黄色部分不等，如下图所示，则可以继续按 Next[Next[i-1]] 的顺序往下找，直到匹配到与 Next[i-1] 值相等的位置 p 此时满足上述两个条件。 Next[i] = p+1 。
因为在没有找到符合上述条件的情况下 p 最终等于 -1，所以在 p == -1 的情况下直接将 Next[i] 设为 0，表示从第一个元素开始匹配，此时 Next[i] == p+1 ，可以与上一段描述找到的情况在代码层面进行合并。
2.4 C++ 代码实现
int kmp_find(const string& s, const string& sub_s){
int ssize = s.size();
int sub_ssize = sub_s.size();
if(sub_ssize == 0) return 0;
vector<int> next(sub_ssize,0);
next[0] = -1;
int p;
for (int i = 1;i < sub_ssize; ++i) {
p = i - 1;
while (1) {
if (next[p] == -1 || sub_s[i-1] == sub_s[next[p]]) {
next[i] = next[p]+1;
break;
} else {
p = next[p];
}
}
}
int i = 0 ,j = 0;
while (i < ssize) {
if(j == sub_ssize) return i - sub_ssize + 1;
if (sub_s[j] == s[i] || j == -1) {
i++;j++;
} else {
j = next[j];
}
}
return -1;
}